Basic Physical Processes of Greenhouse Gas Warming

Before we get to the question of how important greenhouse gas warming by CO₂ is, we should all have a grasp of the basic physical processes involved. That will help us in evaluating how sensitive planetary temperatures are to CO₂.

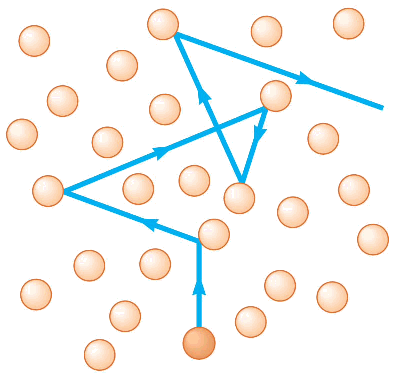
First, let us examine what the meaning of temperature is. The atmosphere is a sea of molecules that are not bound to each other with only space between them. For the moment for explanatory simplicity, let us suppose there is only one kind of molecule. The particles are traveling in differing directions with differing speeds, with the direction and speed of a single particle remaining unchanged until it bangs into another particle. Then the colliding particles will bounce off each other with different directions and speeds than they had before they hit. This is the kind of process that a physicist calls a collision. When a single particle undergoes collisions a great many times, the probability that it is going in any particular direction is randomized; that means the likelihood of it traveling in any particular direction is the same as for all other directions. A multiple-collision process of this sort is called diffusion, and is illustrated in the figure above. In the process of diffusion a single particle will wander in the sea of its fellow particles and change its direction of travel with each collision.

Not only will a particle change its direction with each collision, but it will change its energy as well. If m is the mass of the individual particle and v is its speed, then T = mv²/2 is its kinetic energy.  If one particle in the collision gains energy, conservation of energy would then require that the other particle lose exactly the same amount of kinetic energy. Assuming conservation of energy, and noting that during the collision the sum of the potential energies are essentially constant since the particles are at approximately the same point, then the sum of the two kinetic energies must be constant. Now suppose that we are at a place where the average velocity of the particles in the system is zero. There must be as many particles with negative speeds in one direction as positive speeds. In that reference frame, any speed a particle has is a random, stochastic speed. The discipline of statistical mechanics, takes in these assumptions and calculates that the probability that any single particle has a speed between v and v + dv (dv is a very, very small infinitesimal number over which no function of v varies) is directly proportional to exp[-mv²/(2kT)] dv. In this last expression, k is a universal constant called the Boltzmann constant and T is defined as the absolute temperature of the ensemble of particles in degrees kelvin. Therefore as the temperature increases, one finds significant probabilities of particles having higher and higher speeds. The implication of all this is that as energy is dumped into the system of particles, i.e. they are heated, one will find significant numbers of particles at higher velocities and the temperature T of the system  increases. The temperature T is defined to be a measure of how broad the distribution of random velocities is. The larger the temperature, the larger the random velocity amplitudes at which we can find significant numbers of particles.

Isn’t physics fun! It even makes sense! (A lot more sense than most progressive politicians I know of.)

The next thing to discuss is what all this has to do with global warming. We start with the sun, which provides almost the complete entirety of the available energy at the Earth’s surface. The energy in all fossil fuels is merely stored sunlight. Energy from the sun arrives at the Earth in the form of electromagnetic radiation that is mostly in visible and infrared wavelengths to which the atmosphere is mostly transparent. (That is why our eyes evolved to see in the visible wavelengths). Most of it passes through the atmosphere and strikes the surface of the Earth and is absorbed by ground molecules for a very short period of time ( on the order of 1 to 100 nanoseconds, 1 nanosecond equals 10^-9 seconds. During that short time, the molecules have been knocked into higher energy states by absorption of the incident light on the ground. They then decay from these energy states in a cascade of intermediary states and in the process they emit “particles” of light at infrared wavelengths.

We have now arrived at a very tricky part of my narrative. You see, molecules are the largest physical entities which display some quantum mechanical behavior. In particular they have quantized internal energy levels, i.e. discrete energy levels with no energy states in-between. When a molecule decays from a higher energy level to a lower energy level with a difference of energy ΔE, the released energy is emitted as a “particle” of light, called a photon, at infrared wavelengths and frequencies. The wavelength λ is related to the frequency ν through the relation λν=c, where c is the speed of light. The frequency of the emitted photon is given by ν=ΔE/h where h is a constant called Planck’s constant. The number of these quantized energy states that have differences of energy with other energy states that would allow the emission of infrared photons is necessarily extremely finite and limited. For a greenhouse gas to be a greenhouse gas, it must have molecules with one or more pairs of energy states with this property.

By now, you must be confused with at least a couple of questions. For one thing, how can a “particle” like a photon have wave-like properties? (I told you this would be tricky!) The answer is that quantum mechanical “particles” have very different properties from classical particles. For one thing, if no forces are acting on them, they do not travel in straight lines; they spread out like waves. Only when they are absorbed or emitted do they act somewhat like classical particles. Absolutely every single physical entity on the quantum mechanical level possesses this wave-particle duality. For mathematical reasons, the natural way of interpreting this situation is the wave gives the probability of finding the particle at any one place, and the particle is what the wave collapses into when it is absorbed. When a particle is emitted, it immediately expands into a wave. There are several different competing metaphysical explanations for all this, but an honest statement would be that we really do not understand why reality is the way it is.

Another question you might have is why am I harping about infrared radiation? The answer is that radiation in the infrared frequencies are what can most easily be absorbed and emitted to give kicks to greenhouse gas molecules to speeds that our skin interprets as normal heat. You see, the actual warming of the atmosphere from this radiation occurs when an infrared photon is either emitted or absorbed by a greenhouse gas molecule. When that happens the molecule either absorbs or loses the momentum of the absorbed or emitted photon. (Oh, yes, I forgot to tell you that total momentum is also conserved!). This either adds to or takes away from the random velocity of the molecule, but mostly it adds.This increases the width of the random velocity distribution of the greenhouse molecules and therefore it increases their temperature. Voila! We have Greenhouse gas heating!

The picture we now have of greenhouse gas warming goes something like this. Incident radiation from the sun strikes the Earth, is absorbed by earth molecules and then re-emitted by the earth molecules, primarily in the infrared frequencies away from the Earth’s surface. An infrared photon then travels from greenhouse gas molecule to greenhouse gas molecule in a diffusion process. with its effective path between the molecules much like the figure at the top of this post. Eventually, the photon will diffuse to the top of the troposphere, where the probabilities approach absolute certainty that it will be lost to space.

There is a bit more to tell about this story, but I will close this over-long post here and finish the tale in the next post.

GO TO HOME

Sharing is caring!